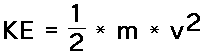 where m = mass of object
where m = mass of objectv = speed of object
 This
equation reveals that the kinetic energy of an object is
directly proportional to the square of its speed. That means
that for a twofold increase in speed, the kinetic energy
will increase by a factor of four. For a threefold increase
in speed, the kinetic energy will increase by a factor of
nine. And for a fourfold increase in speed, the kinetic
energy will increase by a factor of sixteen. The kinetic
energy is dependent upon the square of the speed. As it is
often said, an equation is not merely a recipe for algebraic
problem solving, but also a guide to thinking about the
relationship between quantities.
This
equation reveals that the kinetic energy of an object is
directly proportional to the square of its speed. That means
that for a twofold increase in speed, the kinetic energy
will increase by a factor of four. For a threefold increase
in speed, the kinetic energy will increase by a factor of
nine. And for a fourfold increase in speed, the kinetic
energy will increase by a factor of sixteen. The kinetic
energy is dependent upon the square of the speed. As it is
often said, an equation is not merely a recipe for algebraic
problem solving, but also a guide to thinking about the
relationship between quantities.
Kinetic energy is a scalar
quantity; it does not have a direction. Unlike velocity,
acceleration, force,
and momentum, the
kinetic energy of an object is completely described by
magnitude alone. Like work and potential energy, the
standard metric unit of measurement for kinetic energy is
the Joule. As might be implied by the above equation, 1
Joule is equivalent to 1 kg*(m/s)^2.

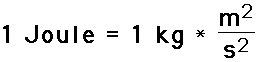
No comments:
Post a Comment
Your Comment is posted.